secondary research, take two
- Jasmine Ah Yong
- May 19, 2021
- 6 min read
additional secondary research pertaining to applications
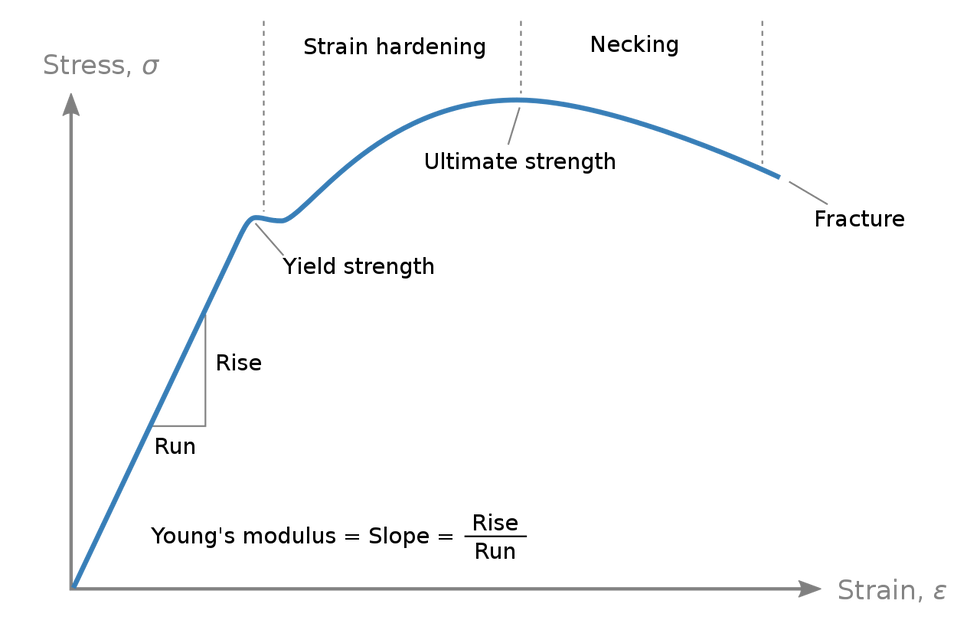
image via Wikipedia
This is still not a formal research hub, nor evidence of completed secondary research. The original blog post for secondary research, which explores general textile physics, can be found here.
tensile strength (Britannica, 2020)
tensile strength: maximum load that a material can support without fracture when being stretched, divided by the orignal cross-sectional area of the material
measured in force per unit area; often expressed in psi, pounds per square inch
when stress is less than the tensile strength are removed, material returns partially or completely to original
when stress reaches the tensile strength, a ductile material forms a constricted region called a neck, where it then fractures
paper making: strength and durability (Britt, 2020)
strength of paper is determined by:
the strength of the individual fibres of the stock
the average length of the fibre
the interfibre bonding ability of the fibre (enhanced by beating and refining action)
structure and formation of the sheet
most papers require a certain minimum strength to withstand treatment received in use, and to permit efficient handling in manufactre
breaking length: the length of a paper strip in metres that would be just self-supporting
varies from 500-14,000 metres
paper products such as towels and sanitary tissue also undergo wet tensile testing
untreated paper possesses about 4-8% of its dry strength when completely wetted
treatment allows wet tensile strength to be raised to about 40% of dry tensile strength
bursting test: the hydrostatic pressure necessary to cause rupture in a circular area of a given diameter
AKA the Mullen test
tearing strength and folding endurance are other tests
stucture has varying degrees of porosity since it is composed of a randomly felted layer of fibre
materials science (Patel, 2018)
the goal of the steel industry is to develop high-strength but inexpensive, "microalloyed" steels with weight savings via thickness reductions
intermediate in composition between carbon steels and alloy steels
low in carbon with minute additions of titanium or vanadium
tensile strengths can be triple the value of the carbon steels they are designed to replace
slight loss of structural stiffness (elastic moduli is the same as other steels)
strength of most plastics (e.g. epioxies, polyesters) is about 20% of steel or aluminum, and their elastic modulus is 1/60 of steel or 5% of aluminum
carbon fibres have extremely high modulus values (up to 5 times that of steel)
cost-prohibitive, so only really used in the aerospace industry
glass fibers have modulus values that can approach 1.5 times that of aluminum
plastic - the polymers (Rodriguez, 2020)
physical state and morphology of polymers have strong influence on their mechanical properties
elongation that occurs when a plastic is loaded in tension
glassy polymers (e.g. polystyrene) is quite stiff -- high ratio of initial stress to initial elongation
highly crystalline plastics (e.g. polyethylene, polypropylene) are usuably as films and molded objects
at room temperature, their amorphous regions are above their glass transition temperature
leathery toughness above T_g results from the crystalline regions that exist in an amorphous, rubbery matrix
elongations of 100-1,000% are possible with these
creep: almost all plastics exhibit some elongation on being stressed that is not recovered when the stress is removed
may be very small for a plastic well below its T_g, but can be significant for a partly crystalline plastic above T_g
toughness: energy absorbed by a polymer before failure, often as the result of a sudden impact
repeated applications of stress below tensile strength of a plastic may result in fatigue failure
flexural modulus: stiffness
tensile strength: breaking stress
reinforcements such as finely divided silica, carbon black, talc, mica, calcium carbonate, etc., can be incorporated as particulate fillers
contribute to stiffness
ultimate tensile strength (Velling, 2020)
ultimate tensile strength: ability of a material to resist tearing due to tension
applies to all types of materials (wires, ropes, metal beams, etc.)
tensile stress at which tearing takes place is the tensile strength
both ductile and brittle materials will approach a point of failure
initially, there will be a uniform deformation observed
eventually, the uniform plastic deformation becomes local concentrated deformation -- necking phenomenon
intensive property -- does not depend on the size of the sample
the same material with varying cross-sectional area will have the same value of tensile strength
stress-strain curves have 4 major regions
proportional limit: specimen acts like a spring and any strain caused is completely reversible
Hooke's region -- Hooke's law is applicable
yield limit: permanent deformation sets in; the specimen will not return to its original dimensions
strain hardening region: microstructure of the material is modified; material becomes harder and tougher
at its strongest point
necking region: local reduction in cross-section; material only moves towards failure
knowledge of tensile strength is imperative to ensure the material is the right choice for an application
ensures an incident-free service life (e.g. roof constructure should be able to withstand a normal snow load)
tensile strength is measured by a Universal Testing Machine
specimen is held on opposite ends using clamps; one of the ends remains stationary while the other is pulled at a steady increase of force
the SI unit is N/m^2 or Pascal
how to measure tensile strength, elastic modulus, and ductility (n.a., n.d.)
"to find out how strong a wire is, one could just hand heavier and heavier weights on it until it breaks" -- so it's totally a valid option!
a bigger wire will take more pounds to break than a smaller one, so stress is measured by the number of pounds pulling on the wire, divided by the cross-sectional area
after reading this so many times, I'm kind of questioning the idea of experimenting with different thicknesses of yarns at all, especially given that I don't have the resources to make super specific measurements regarding cross-section; this is therefore getting relegated to 'side-priority-I'd-be-happy-to-get-to-but-not-necessary'
% elongation: the amount the specimen streteches before breaking
from 2 to 2-3/4, there is a 3/4 difference, so 3/4 divided by 2 is a 0.375 stretch of 37.5% elongation
could document this, but I don't think it'd work very well
Young's modulus is the slope of stress vs. strain
yield strength: point at which the specimen takes a permanent stretch
significance and use of the tensile test in various industries (2018)
aerospace and aviation
lightweight materials that can reduce fuel comsumption but still satisfy strength requirements
strength of adhesive bonds, carpets, cables, gaskets, hoses, seat belts, wiring looms, harnesses, etc.
automotive
breaking strength of seat belt and car seat's foam ribber
assessing quality of exterior (e.g. door and window seals, mirrors, mud flaps, bumper moldings and trums) and interior (e.g. airbags, dashboards, handles, mirrors, handbrake levers) fittings
metals and constructure
strength of safety support nettings, timbers, geotextiles, and bond strength of adhesives, sealants, mastics, etc.
electrical and electronics
conductive film and substrate used in flexible electronics
tensile strength of printed circuit board materials and electrical wires
withdrawal force of connectors
medical equipment and materials
strength of lenses to guarantee functional everyday use
surgical tubes, catheters, etc. must be able to properly control junctions, etc.
properties of bandages, dressings, and other textile materials
elongation of surgical gloves, silicone rubbers, etc.
strength of needles, injectors, respiratory masks, and IV connector fittings
packaging and paper
elongation and strength of plastics, board, or paper
maximum load
how easy or difficult it is to open packaging
force required to tear a seal, adhesive bond, or label
folding properties
plastics and rubber
must have enough strength to withstand external physical stress
important to identify elongation and necking or yield strength of products
strength of interlocking components
adhesion of plastic and rubber labels
quality control
sports and fitness
production of strings, as well as knot strength and elongation of strings (tennis, etc. rackets)
strength of thermoplastic elastomers and vulcanized rubbers in solves of footwear and equipment
tear and tensile strength of fabrics using in performance footwear, apparel, and equipment
textiles
assessing strength to be wearable and withstand daily use
breakage strength, tear resistance, and elongation of natural and synthetic fabrics, thread, yarns, cords, and ropes
strength of vulnerable seams
pull-off proeprties of buttons, zip fasteners, stiched decorations, etc.
There's honestly still a lot more reading I'd like to do, but this seemed like something of a natural stopping point for now (especially given that I need to turn in something sooner than later). I should probably do a bit more reading on yarn/rope specific tensile strength (i.e. the theory behind different behaviours), although that doesn't necessarily need to be done before experimentation, and it might even be better if I do it after (so that confirmation bias doesn't impact my results).
Realistically, 'tensile strength' is way too broad a horizon to consider. Which is, in hindsight, pretty much the most obvious statement ever. Reflecting a bit more on my project, I decided that what I'm really focusing on is how to get the most strength out of a given material. While I'd rather focus primarily on fibrous materials -- so no steel cables or the like -- I think that there's just a lot more literature for secondary research on. In future, I will try to look into the tensile strength of specific fibrous materials, and their usage in structures such as hammocks, rope bridges, etc.
I am also slowly growing convinced that it might be better to focus on elastic modulus given the context of my project (i.e. textile work), but there inevitably arises the issue of my being able to at least semi-accurately measure these kinds of values. For that reason, I still don't think modulus is a realistically measurable value.
In any case, I've still got a day or two until I can start primary investigation, so I should be able to get a bit more research done, though probably not enough to reasonably post.




Comments